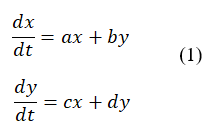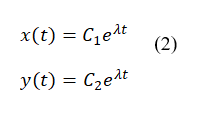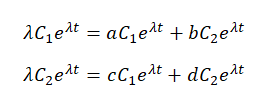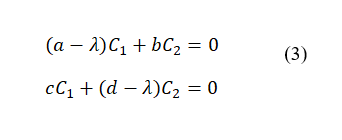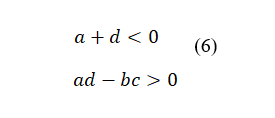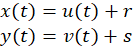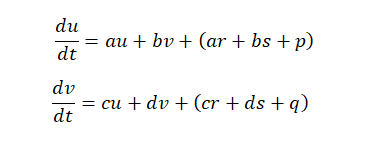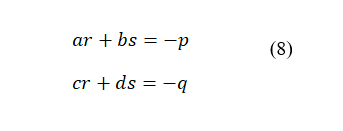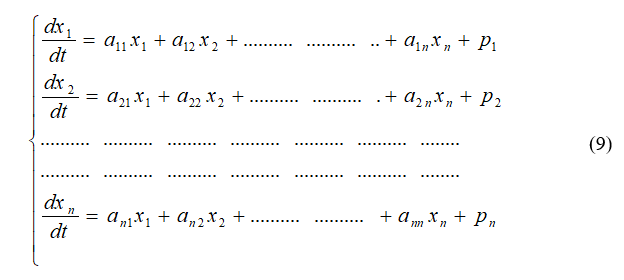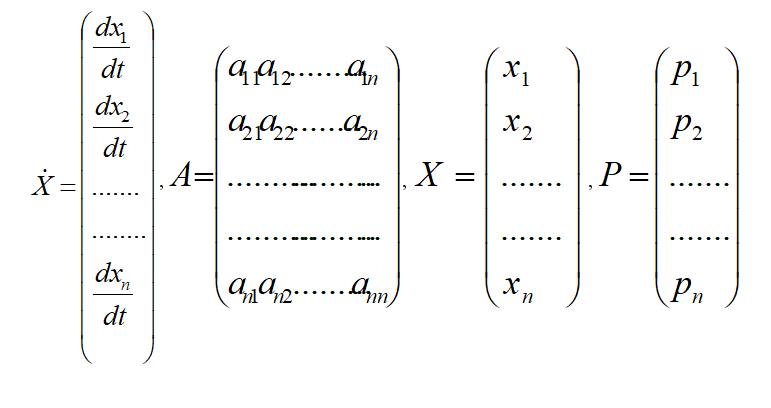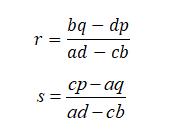Везде
Математическая модель оценки устойчивости и динамики инновационной деятельности
Оглавление
Аннотация Оценить Содержание публикации
Библиография Комментарии
Поделиться
QR
Метрика
Математическая модель оценки устойчивости и динамики инновационной деятельности
Аннотация
Код статьи
S020736760004135-7-1
DOI
10.31857/S020736760004135-7
Тип публикации
Статья
Статус публикации
Опубликовано
Авторы
Иванова Вера  
Аффилиация: Федеральный социологический центр РАН
Адрес: Российская Федерация, Москва
Выпуск
Выпуск 2
Страницы
43-63
Аннотация

Статья посвящена вопросам моделирования процессов саморазвития при реализации инновационных проектов на основе социальных и экономических прямых и обратных связей. С целью разработки стратегий инклюзивного развития и минимизации рисков при запуске инновационных проектов разработана математическая модель в виде системы двух дифференциальных неоднородных уравнений первого порядка, описывающая динамику инновационного развития. Модель позволяет выявить критерии устойчивости запуска инновационной деятельности в зависимости от интенсивностей социальных и экономических обратных связей, а также иллюстрирует отсутствие непосредственной количественной зависимости устойчивости такого развития от наличия и величины прямых положительных либо отрицательных связей обоих указанных видов.

Ключевые слова
математическая модель, инновационная деятельность, инклюзивное развитие критерий устойчивости, прямые и обратные связи, социальные и экономические связи, начальные условия, динамика развития, социальные отношения, неоднородные дифференциальные уравнения, метод Рунге-Кутты, годограф скорости
Источник финансирования
Исследование выполнено при финансовой поддержке РФФИ. Проект «Теоретико-методологические основы формирования стратегии инклюзивного развития экономики России» № 17-02-00040 «а».
Классификатор
Получено
14.03.2019
Дата публикации
14.03.2019
Всего подписок
89
Всего просмотров
1438
Оценка читателей
0.0 (0 голосов)
Цитировать   Скачать pdf
1 Инновационная деятельность, также как и любой социально-экономический проект предполагает наличие в процессе его реализации рисков. Последние могут иметь как экономические, так и социальные причины. При этом и те, и другие могут быть двух видов – риски достаточности ресурсного потенциала и риски обеспеченности потенциала саморазвития. Если ресурсные риски, как риски традиционные для оценки, и достаточно «осязаемые» в понятийном плане, давно уже являются основой самых различных технико-экономических обоснований, то риски, точнее пока лишь их отдаленные аналоги, по обеспечению запуска механизмов саморазвития – только начинают входить в арсенал прогнозных оценок для инновационных проектов. Математический аппарат ресурсных рисков в основном базируется на двух понятиях - ожидаемого значения случайной величины и вариации (дисперсии) той же самой случайной величины. Последнее понятие как раз и принимается здесь за меру риска [1]. Риски же обеспеченности потенциала саморазвития в процессе реализации инновационного проекта не только не выявлены математически, но пока еще не сформулированы даже на методологическом уровне. Одна из основных причин этому – отсутствие адекватной модели и соответствующего ей математического метода по описанию процессов саморазвития применительно к социально-экономическим системам. Пока же явление саморазвития применительно к инновационной деятельности рассматривается на уровне только лишь парадигмы «саморазвивающейся среды» [2. С.17]. Тогда как актуальность прогнозных оценок результатов, а также динамики инновационной деятельности только усиливается [3]. Именно поэтому в статье предложено обоснование модели инновационного социально-экономического саморазвития и на ее основе – математический метод оценки устойчивости и динамики развития инновационной деятельности в зависимости от условий и факторов функционирования институциональной среды.
2 Обоснование методологического подхода. В качестве основного методологического подхода для реализации целей и задач настоящего исследования будем рассматривать инновационную деятельность как саморазвитие системы с прямыми и обратными социально-экономическими связями [4], а собственно социальные отношения в рамках такой системы - как динамический комплекс прямых и обратных положительных и отрицательных связей только социального типа [5]. В качестве источника прямых и обратных социальных связей будем рассматривать феномен "знания" [6]. Это обусловлено тем, что при производстве знания как нового ресурса и нового товара, наделенного, как минимум, тремя фундаментальными противоречиями, появляются отрицательные обратные связи в инновационной деятельности. Прямые же связи, проявляющиеся в той же инновационной деятельности, формируются уже в процессе эволюции общества на основе ранее накопленного знания в виде социального опыта [7].
3 Заметим, что инновационная деятельность, как деятельность, направленная на реализацию экстернального эффекта в хозяйственной системе, предполагает наличие в этой системе прямых и обратных связей как экономического, так и социального видов. Их не надо путать с внутренними деловыми связями между индивидами в коллективе. Если обратные социальные связи, возникающие в результате разработки нового инновационного продукта, реализуются в самом коллективе разработчиков, то обратные экономические связи реализуются в виде экстернального эффекта вне такого коллектива.
4 Специфика прямых социальных связей, которые в основном относятся к отрицательному виду, состоит в том, что они, с одной стороны являются тормозом для выстраивания творческой атмосферы в научном коллективе, а с другой – именно они, точнее их разнообразие, определяет спектр индивидуальных творческих начал в психике отдельного индивида. А без последних творческий коллективный труд вообще не возможен.
5 Основу в качестве источника здесь составляет тот социальный опыт, что индивид лично получил в предыдущие периоды своей социальной жизни. Для россиян он в большой степени будет определяться опытом перестройки. С точки зрения творческого потенциала, психологически опосредованной активности - окраска тех эмоций, что индивид пережил в результате перестройки – не столь важна, важна их глубина и устойчивость в воспоминаниях. Однако эта самая эмоциональная окраска предопределяет, с другой стороны, сущность социальных отношений в коллективе. Более подробно и конкретно этот перестроечный опыт, который получили россияне, и его последствия описаны в ряде работ А. Иванова [8; 9; 10].
6 Но есть и другая сторона сегодняшней российской действительности. Ведь стрессы и неприятности по жизни, что пережил индивид, как раз и дают возможность развиваться его ассоциативному мышлению. Эти невзгоды, негодования, переживания и возмущения – обязательные атрибуты полноценного жизненного опыта. Но, конечно, лишь в пределах, за которыми уже идет деградация и распад личности. То есть существует определенная грань, до которой человека можно довести в лишениях и невзгодах с целью его подготовки для творчества и активной жизненной позиции.
7 Другие виды отрицательных прямых связей имеют своими корнями эпизоды и целые исторические периоды в эволюции цивилизаций и отдельных государств [11. С. 241]. Здесь же укажем только на один общий для многих стран момент, являющийся источником отрицательных прямых социальных связей в коллективах, работающих над инновационными проектами. Так, многие военнослужащие, демобилизовавшись из армии, не могут построить карьеру на гражданской службе: сталкиваются с культурными противоречиями и не могут найти применение навыкам, полученным на военной службе. Основная причина этого – бывшим военным бывает нелегко научиться строить горизонтальные деловые связи, т.к. они привыкли к строгой вертикальной иерархии [12].
8 Любое развитие, как форма существования динамической системы, должно быть наделено обратными связями, величина и изменения которых со временем определяют устойчивость указанного развития. Такая устойчивость может пониматься и как вообще способность к развитию, т.е. качественному изменению, так и как способность развиваться без скачков, в том числе регрессионных срывов. Последние возникают в тех случаях, когда как положительные, так и отрицательные обратные связи по какой-либо причине резко меняют свои относительные значения. Тогда-то и может произойти срыв, чреватый, в том числе и полным разрушением рассматриваемой динамической системы. Именно этот случай является наиболее опасным с точки зрения теории управления. А на практике, например в отношении кредитно-денежного обращения, он трактуется как хорошо известный финансовый кризис. Особенностью инновационного развития эпохи постиндустриального типа воспроизводства, когда ключевой продукт – знания, является наличие сильных положительных обратных связей вследствие действия экстернального эффекта [13]. Последний предполагает, что знания как нерастрачиваемый ресурс, произведенный одним производителем, может быть использован в производственных процессах других производителей, что порождает процессы типа цепной реакции и, естественно, очень сильно интенсифицирует экономику страны. Естественно было бы предположить, что при планировании запуска инновационного продукта в виде новых знаний появится возможность учитывать и положительные воздействия на экономику такого продукта в смежных ее областях.
9 И именно так и поступают, когда принимают решения на уровне государства. Но здесь-то и появляется опасность неустойчивости. Ведь ожидания воздействия экстернального эффекта на смежные отрасли могут не оправдаться, т.к. опыта, как правило, еще такого нет, а ресурсы из этих отраслей уже изъяты, да и время прошло. Возникает критическая ситуация, влекущая за собой затяжной кризис. Именно с таким кризисом Россия столкнулась в последнее время, возложив ранее большие надежды на закон о техническом регулировании [4]. Принятие этого закона, как считают многие специалисты в области стандартизации, является стратегической ошибкой государства [14]. Вместо планировавшегося принятия около 700 регламентов, которые должны были иметь силу закона и приниматься на уровне правительства и Президента, за семь лет было принято только 11. В настоящее время в России действует всего 16 технических регламентов [15]. При этом система российских стандартов, позволявшая все делать на лучшем уровне – была заброшена фактически с отменой обязательности следования большинству из этих стандартов, а техническое регулирование в стране осталось без нормативной базы. При этом каждый производитель сейчас волен делать свою продукцию так, как он считает это нужным лично ему самому, без учета интересов страны. А каждый чиновник может ставить этому производителю свои условия получения того или иного разрешения (отвод земель, согласование допустимых производственных выбросов и т.п.) и взимать при этом в виде подношений свою административную ренту.
10 Это все можно охарактеризовать как первый опыт системного кризиса в нашей стране, связанного с недооценкой как проблемы ресурсного обеспечения инновационного развития в условиях постиндустриального типа воспроизводства, так и недооценкой действующих при этом обратных связей. В результате получились полнейший хаос и неопределенность. На сегодняшний день принят закон «О внесении изменений в Федеральный закон «О техническом регулировании» [16]. Но это, как считают трое бывших председателей Госстандарта, очередная ошибка. Первая была с самим принятием закона о техническом регулировании, сейчас совершена вторая. Пройдет еще год, два, три и снова будут говорить, что закон не удался, напрасно потрачены 7 лет. За это время можно было бы техническую революцию сделать. Те деньги, что потрачены на первичный закон можно было бы использовать на обновление и разработку новых стандартов и большую часть их гармонизировать с зарубежными стандартами. При этом мы могли бы в течение двух лет, максимум трех лет, стать самыми лучшими в мире в области технического регулирования. В настоящее время организован сбор подписей под обращением к президенту РФ об отмене Закона «О техническом регулировании» и замене его на законы «О стандартизации», «О сертификации» и «О государственном контроле (надзоре)». В них должны быть, в частности, четко прописаны критерии выбора предметов нормативно-правового регулирования и самого регулирования.
11 Но вернемся немного в прошлое. Реформа технического регулирования изначально рассматривалась как один из элементов дебюрократизации экономики. Когда принимался Закон «О техническом регулировании» актуальность его связывали со вступлением России в ВТО, а собственно принятие закона рассматривалось в первую очередь как политический шаг, и только после этого в принципе можно было бы рассчитать и его экономический эффект. Закон был продавлен без соответствующего технико-экономического обоснования, которое предполагало выявление экономических аргументов для двух альтернативных вариантов: 1) система регулирования промышленного производства, доставшаяся нам от Советского Союза, была основана на ГОСТах и на ведомственных нормативных актов, у нее были определенные минусы, в первую очередь из-за большого количества собственно документов и, во-вторых, из-за того, что требования этих документов не всегда выполнялись, т.к. документы эти не обладали в большинстве своем силой закона. Однако система все же работала, и следовало, естественно, оценить уровень потерь для страны в случае утраты такой целостной системы; 2) одновременно следовало оценить, сколько страна может приобрести в экономическом плане при переходе к техническим регламентам и уже на основе баланса возможных потерь и приобретений необходимо было решать вопрос о правомерности внедрения технических регламентов вместо ГОСТов.
12 Много было аргументов за и против. Однако количественных оценок так и не прозвучало. Технико-экономическое обоснование вообще проведено не было, потому что не было методологической базы. И на вопрос, как оценить эффективность реформы по смене форм технического регулирования, никто не взялся ответить количественно. Получилось так, что старая система была развалена, а новая не создана. И именно такой исход вообще не рассматривался. Таким образом, налицо серьезный системный кризис, охвативший правовые вопросы воспроизводства в стране в целом, и никто даже не предполагал, что так получится. Системность его определяется как отсутствием адекватной законодательной базы для технического регулирования в стране, отсутствием компетентных функционеров в законодательных сферах, а также отсутствием обратных положительных связей между этими функционерами и представителями общественности. Все это подтверждает тезис, что нужна научная методология технико-экономического обоснования больших проектов по инновационным наукоемким продуктам, таким как технические регламенты, необходимо финансовое прогнозирование объема бюджетных средств, а также объема и качества кадровых ресурсов, привлеченных для разработки адекватной метрологической базы по обеспечению работоспособности принимаемых регламентов в РФ. На сегодня серьезной проблемой является перспектива практической работоспособности тех ГОСТов, из которых были изъяты обязательные требования, перенесенные в дальнейшем в новые технические регламенты.
13 Несмотря на все методы, имеющиеся в экономическом активе, модели прогнозирования очень сложны и, как показала реформа технического регулирования, здесь надо учитывать и материальные, и административные потери, которые вытекают из структуры прямых и обратных связей при инновациях, в частности, в государственном секторе. И, конечно же, здесь необходима самая бескомпромиссная борьба с коррупцией. Эта борьба должна стать основой всех начинании.
14 Новые возможности, которые дает на практике экстернальный эффект в условиях России, привели к плачевным результатам, произошел тот самый регрессионный срыв, т.е. система технического регулирования потеряла устойчивость и попросту разваливается на глазах, а это вполне может привести и к развалу вообще всей отечественной промышленности. Системность кризиса с техническим регулированием предопределяет и необходимость системного подхода к анализу его первопричин. Одна из таких первопричин системности кризиса – отсутствие признания легитимности частной собственности, приобретенной в процессе приватизации, со стороны большинства российских граждан. В РФ собственность нации была экспроприирована безвозмездно – чисто административными средствами, даже без видимого диалога и переговоров. Это – первородный грех нынешнего частного промышленного капитала России. Этот грех не стали искупать хотя бы в виде символического осуждения той приватизации. Конфликт загнали в глубины коллективной памяти. И он напоминает о себе через подобные кризисы, т.к. чиновники, памятуя, что мошенничества при приватизации им простили, перестали с кем-либо и с чем-либо считаться вообще. Население же в отместку за это им абсолютно не доверяет ни в чем, и сотрудничать с ними не желает. А это значит, что институты гражданского общества попросту не функционируют и так нужные положительные обратные связи в обществе не реализуются.
15 С хозяйственной точки зрения приведенный выше пример связан с вводимым в обиход в экономической науке термином «открытые инновации». Этот термин предполагает использование ранее кем-то разработанных, а часто и опробованных, инноваций другим экономическим агентом, причем часто в совершенно новых условиях. С одной стороны, этот подход ускоряет технический прогресс, но, как это оказалось в данном случае, представляет опасность для нового пользователя такими инновациями в виде возможности банкротства последнего.
16 Математическая модель инновационного развития. Ниже попытаемся на основе достаточно простой математической модели обосновать принципиальную возможность такого неблагоприятного исхода и очертить тот круг параметров модели, соответствующих уровню материально-правового обеспечения вновь внедряемого проекта, который ответственен за его устойчивость.
17 Как уже упоминалось выше, инновационное развитие характеризуется наличием сильных положительных обратных связей. Естественным было бы предполагать, что также сильными будут в его структуре и отрицательные обратные связи. Как те, так и другие в таком случае будут развиваться по экспоненциальному закону. Обозначим через параметр x количественную величину, характеризующую текущие результаты инновационного развития в виде, например, увеличения выпуска продукции, ее качества, расширения сети представительств фирмы и т.п. на какой-то момент времени. А через параметр y - количественную величину вновь существующих на тот момент времени в процессе инновационного развития эффектов, тормозящих это самое развитие, в частности, коррупцию, взимание институциональной ренты и т.п. Через параметры и , соответственно, обозначим производные по времени двух введенных нами выше параметров. При этом динамика во времени первого параметра будет характеризоваться интенсивностью, например, положительных обратных связей, а второго – отрицательных. Поскольку выше мы на основе действия сильных обратных связей обосновали экспоненциальный характер развития того и другого параметра, то логично предположить, что динамика каждого из них будет характеризоваться совместным воздействием на инновационный процесс текущих значений этих двух исследуемых нами параметров. В частности, в виде их суммы с различными долевыми составляющими, описываемыми, в первом приближении, постоянными коэффициентами a, b, c, и d. Сказанное позволяет нам сформулировать базовую динамическую модель инновационного развития в условиях постиндустриального типа производства, в том числе, с использованием открытых инноваций.
18 Рассмотрим систему линейных дифференциальных уравнений:
19

20 Решение (1) будем искать в стандартном экспоненциальном виде
21

22 Подставляя (2) в (1), получим
23

24 Или
25

26 Система уравнений (3) для C1 и C2 имеет нетривиальное решение, только если выполняется условие равенства нулю детерминанта матрицы (3) ,
27 то есть . (4)
28 Для устойчивости решения системы (1) необходимо, чтобы все корни характеристического полинома (4) имели отрицательную действительную часть
29 (5)
30 Согласно критерию Гурвица (или просто по теореме Виета) условие (5) выполняется, если
31

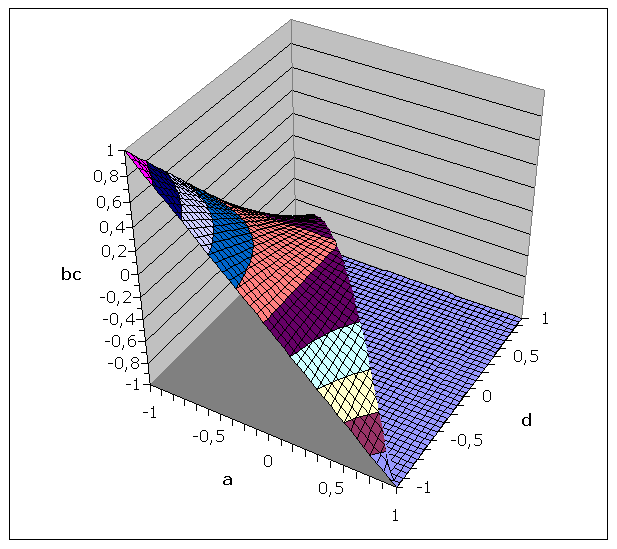
32 Условие ad-bc>0 гарантирует, что система (1) имеет только одно положение равновесия x(t)=y(t)=0. То есть в области равновесия (в ее математической трактовке) наша система из любого начального условия со временем перемещается в нулевое положение. Здесь следует заметить, что математическая трактовка устойчивости прямо противоположна трактовке устойчивости в ее экономическом аспекте. Последняя соответствует в лучшем случае стагнации экономики, а в худшем – ее коллапсу. Математическая же неустойчивость соответствует именно экономическому развитию, когда система из какого-то начального условия со временем переходит в новое положение. Таким образом, для устойчивого развития (в экономическом смысле) условие (6) должно быть записано с противоположными знаками неравенства. В свою очередь такое условие определяет область на Рис. 1, которая находится выше изображенной на этом рисунке криволинейной поверхности и правее вертикальной диагональной плоскости, проведенной внутри рассматриваемого квадранта.
33 Таким образом, не рассматривая функциональные модели инновационного развития, на основе которых формируются собственно стратегии управления таким развитием, мы на модели, привязанной лишь к структуре обратных связей, смогли сформулировать один из основных критериев подобных стратегий управления. Кратко его можно изложить в следующей редакции: ресурсное обеспечение инновационного развития должно быть выше критического уровня, который разделяет область собственно развития инновационного проекта и область его краха.
34

Рис. 1. Границы области устойчивости в положительном квадранте трехмерного координатного пространства a, d, bc
35 Здесь следует отметить, что "устойчивое развитие" мы понимаем как развитие хозяйственной системы с неотрицательным выходом итогового продукта (товара). При "устойчивом инновационном развитии" в качестве итогового продукта выступает продукт с инновационными свойствами, которые определяются наличием у такого товара (продукта) экстернального эффекта, распространяющегося по типу цепной реакции у потребителей такого товара, т.е. вовне собственного инновационного производства.
36 В свою очередь, экстернальный эффект обязан исключительно феномену знания, входящему составной частью в инновационный продукт в виде товара. Таким образом, "устойчивое инновационное развитие" - это производство товаров с экстернальным эффектом (проявляющимся у потребителей), который задействуется в экономике через положительные обратные связи. Критерием устойчивости инновационного развития выступает комплекс величин интенсивностей таких обратных связей - как положительных, так и отрицательных. В нашем случае эти величины интенсивностей не что иное, как коэффициенты a, b, c и d в нашей системе двух уравнений (1), т.е. коэффициенты, отвечающие за обратные связи. В отличие от чисто экономических связей, мы рассматриваем еще и связи социальные. При этом обратные их виды также дают экстернальный эффект, но уже не у хозяйствующего потребителя инновационного товара, а в самой производящей системе (творческом коллективе), где и происходит инновационная деятельность по производству знания как инновационного товара. Эти обратные социальные связи также описываются величинами их интенсивностей и своими знаками (положительными либо отрицательными) через указанные выше четыре коэффициента в системе двух дифференциальных уравнений первого порядка. Эти коэффициенты в общем случае объединяют для каждого x и y как экономические, так и социальные связи.
37 Добавляя в систему двух уравнений (1) свободные члены p и q, ответственные за прямые связи (также могут быть как положительными, так и отрицательными), которые могут рассматриваться как комплексы связей экономических и социальных, а могут быть и чисто социальными в условной постановке так называемой усеченной модели (без экономики), получаем систему двух неоднородных уравнений:
38
  • Сделаем замену переменных:
39

40 и найдем такие значения r и s, чтобы система (7) стала однородной относительно новых переменных u(t) и v(t):
41

42 Если r и s удовлетворяют системе алгебраических уравнений:
43

44 то не трудно заметить, что система уравнений (7) становится однородной, и к ней применимо условие устойчивости (критерий устойчивости) (6). Таким образом, наличие свободных членов не влияет на устойчивость системы. Заметим, что для устойчивой в математическом понимании системы (7) величины r и s являются асимптотиками функций x(t) и y(t) при условии, что .
45 Для расширения системы (7) на большее число исследуемых динамических параметров, в частности до n переменных, число уравнений и их вид будет следующим:
46

47 Удобно ввести матричные обозначения:
48

49

В этих обозначениях система уравнений (9) приобретает следующую матричную форму:

50 Решение системы уравнений при переменных параметрах более двух, уже не позволит наглядно интерпретировать результаты, хотя и даст возможность упростить оценку интенсивностей связей, поскольку исключит необходимость процедуры свертывания таких интенсивностей в обобщенные величины.
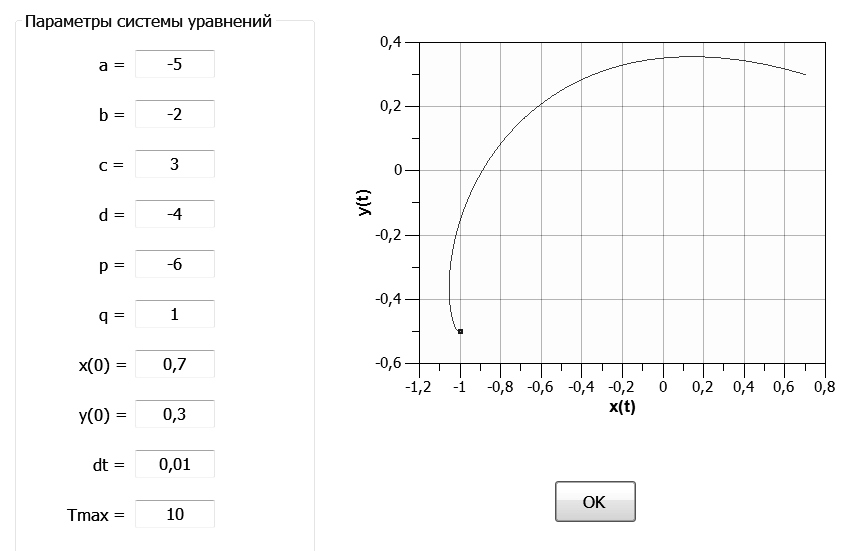
51 Апробация модели на основе расчетов с условными параметрами. На Рис.2 и Рис.3 представлены два варианта модельных решений системы двух дифференциальных неоднородных уравнений первого порядка (7) численным методом Рунге-Кутты (в устаревшей литературе встречалось неправильное название: метод Рунге-Кутта как численный метод решения задачи Коши для обыкновенных дифференциальных уравнений и их систем). Напомним, что прямые связи – это внешняя среда инновационного развития, т.е. институциональная среда, локальная институциональная логика, правовая система, коррумпированность общества и т.д. Как следует из сравнительного анализа кривых на Рис.2 и Рис.3, при изменении значения величины свободного члена p в первом уравнении системы (7) со значения, равного -6, до значения, равного -1, претерпевает значительное изменение, как форма годографа скорости, так и его средняя величина, особенно на начальном этапе. Со своей стороны, внешняя среда сама является производной от этапов эволюции мирового сообщества и, кроме интенсивностей прямых социальных и экономических связей, такая эволюция определяет и конкретную начальную точку возможного инновационного развития, т.е. собственно значение x(0), y(0).
52 Эти прямые связи не определяют критерии устойчивости, т.е. возможности для данной системы, производящей инновационный товар, в принципе начать развитие. Они определяют (но не являются ее точными координатами) только точку равновесия, т.е. до какого момента система «схлопнется» при неустойчивом инновационном развитии, а также влияют на динамику (скорость) устойчивого инновационного развития на его начальных этапах и на траекторию такого развития в координатах x-y, т.е. определяют форму годографа скоростей. Проще говоря, прямые связи ответственны за форму и динамику кривой разворота в начальной фазе инновационного развития.
53

Рис. 2. Устойчивое развитие для системы уравнений (7) согласно модельной расчетной программе при значении свободного члена в первом уравнении p=-6 (движение из начальной точки в направлении увеличения параметров x и y)
54 Рис.3. Устойчивое развитие для системы уравнений (7) согласно модельной расчетной программе при значении свободного члена в первом уравнении p=-1 (движение из начальной точки в направлении увеличения параметров x и y)
55

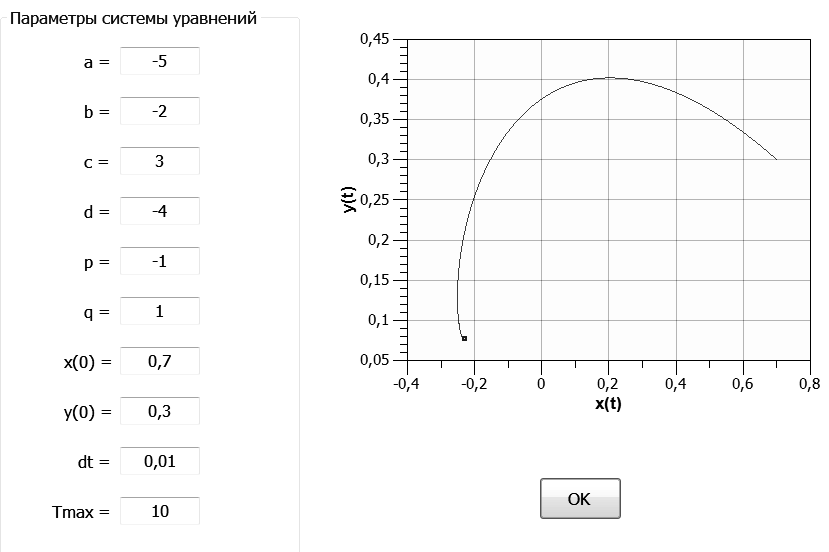
Рис. 4. Неустойчивое развитие для системы уравнений (7) согласно модельной расчетной программе при значении свободного члена в первом уравнении p=-6 и значениях коэффициентов: a=-5, d=-4 (движение из начальной точки в точку равновесия)
56

Рис.5. Неустойчивое развитие для системы уравнений (7) согласно модельной расчетной программе при значении свободного члена в первом уравнении p=-1 и значениях коэффициентов: a=-5, d=-4 (движение из начальной точки в точку равновесия)
57

Рассмотрим другие особенности точки равновесия для системы (7). Решив систему уравнений (8) относительно r и s, получим их выражения в виде дробей:

58 Расстояние R от точки равновесия (r,s) до начальной точки (x0, y0), равное корню квадратному из суммы квадратов (r-x0) и (s-y0), как раз и будет определять динамику процесса во времени:
59 .
60

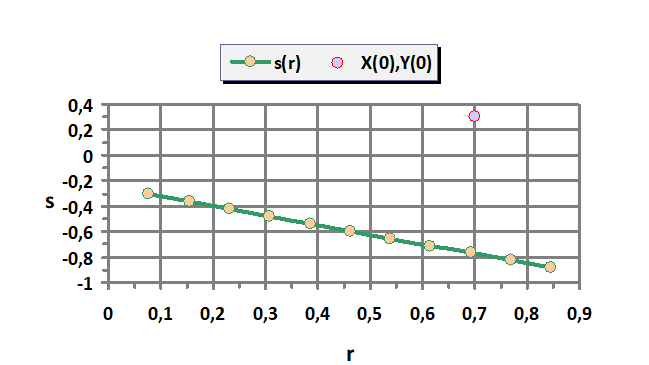
На Рис. 6 представлен график значений величины R при изменении параметра p от минус 1 до минус 6, а также – траектория перемещения точки равновесия при таком изменении. 
61

Рис. 6. Значения величины R и перемещение точки равновесия s(r) при изменении параметра p в диапазоне (-1; -6) при сохранении остальных параметрах в соответствии с табл. 1
62 Подводя итоги, можно сказать, что сегодня, как никогда, наблюдается наиболее острое влияние социальных факторов на научно-исследовательский, творческий по своей сути, процесс [17; 18]. И именно поэтому необходимо учитывать зависимость развития инновационной деятельности от социальных отношений, складывающихся в процессе создания нового продукта.
63 Таким образом, структурирование спектра социально-экономических связей позволяет подойти к анализу устойчивости и динамики инновационной деятельности с использованием математической формализации [19]. Однако такая формализация затруднена из-за невозможности согласования размерностей. Интенсивность связей разного вида, очевидно, предполагает и различную размерность при их описании. Однако в системе неоднородных дифференциальных уравнений первого порядка, описывающей динамику такого инновационного развития, указанные величины интенсивности связей необходимо указывать в единой размерности. Хотя чисто формально показатель интенсивности обратной связи и записывается в виде числа (коэффициента перед тем либо иным целевым показателем) с размерностью обратного времени, но фактически этот коэффициент соответствует приращению целевого показателя, перед которым он стоит, за единицу времени. То есть этот коэффициент косвенно нормирован через размерность того целевого показателя, перед которым он стоит в конкретном дифференциальном уравнении. Что касается прямых связей, которым соответствуют свободные члены в системе уравнений, то в данном случае они имеют точную формальную размерность того целевого переменного показателя, производная которого присутствует в конкретном уравнении. И самая проблемная задача - выразить целевые показатели-функции экономического и социального вида через единую размерность. Из этого следует необходимость поиска единых показателей как для интенсивности самих связей разного вида, так и для целевых аналитических и управленческих показателей чисто экономической и чисто социальной направленности. В частности, с целью рассмотрения динамики инновационной деятельности как деятельности, направленной на реализацию экстернального эффекта по типу цепной реакции в хозяйственной системе [20] на качественном уровне, достаточно системы из двух неоднородных дифференциальных уравнений первого порядка и соответствующим им двух целевых показателей – x и y. Возможны два варианта описания инновационной системы этими показателями: - за x принимаем экономические показатели, а за y – показатели институционального вида, в частности, социальные; - за x принимаем величину целевой функции в виде экстернального эффекта в экономическом и институциональном хозяйственном пространстве, а за y – величину функции торможения, препятствующую реализации такого экстернального эффекта.
64 Расчетные параметры модельной динамики инновационной системы для любого из двух указанных выше вариантов описания такой системы представлены на Рис. 7, Рис. 8 и Рис. 9 и могли бы успешно быть использованы для целей планирования запуска инновационных проектов и прогнозирования их итогов. Однако вроде бы как очевидный путь – использовать стоимостной (через стоимость, выраженную в деньгах) подход к описанию размерности как экономических, так и социальных показателей – оказывается во многом просто тупиковым. Самый главный здесь гносеологический подвох – в наличии большой степени иррационализма в поведении тех самых экономических агентов, а тем более – творческих личностей [21]. Сущность же и универсальность самих денег в экономике – в их свойстве рациональности, порой, правда, приписываемой им далеко не заслуженно. Вторая проблема совмещения экономических и социальных связей – методологическая, заключающаяся в сложности стоимостного измерения конкретного социального поступка (действия). И третья, уже чисто техническая по сути проблема – проблема оценки, опять же в стоимостном измерении, последствия того либо иного социального действия на уровне законченного инновационного проекта.
65 Таблица 1 Исходные параметры для расчетов. Здесь Xeq, Yeq – координаты точки равновесия, x(0), y(0) – координаты начальной точки, Tmax – характерное максимальное расчетное время, dt – шаг расчетов по характерному времени
a = 5 b = -2
c = 3 d = 4
p = -6 q = 1
x(0) = 0.7 y(0) = 0.3
dt = 0.01 Tmax = 10
Xeq = 0.8462 Yeq = -0.8846
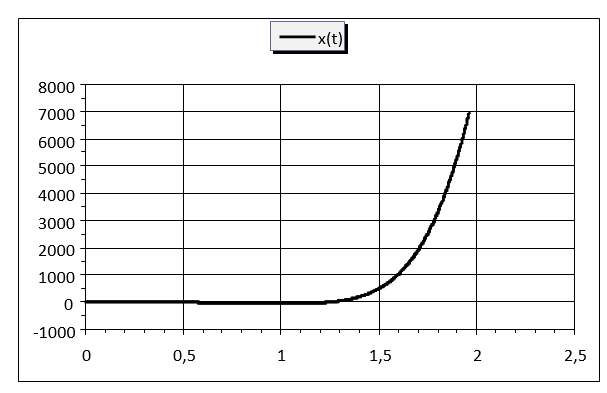
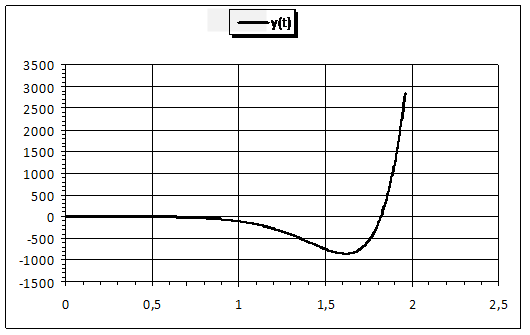
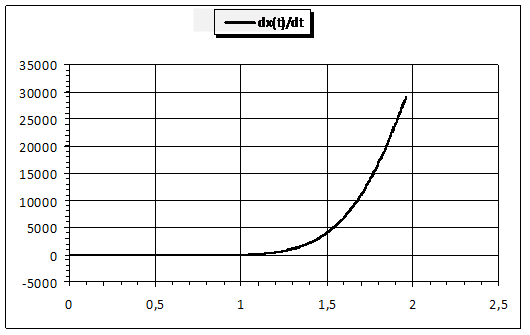
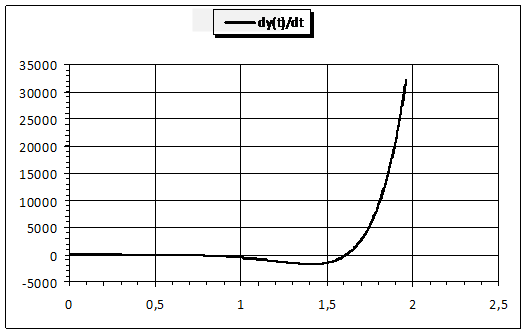
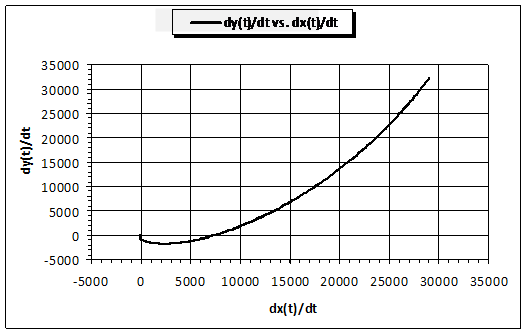
66 Параметры, в вышеприведенной таблице, точно соответствуют исходным данным для расчетной кривой на Рис. 2, где было представлено взаимное соответствие обеих переменных x и y во времени на интегральном уровне. С целью более детальной иллюстрации возможностей расчетной модели, а также для оценки ее чувствительности на различных временных интервалах внутри максимального расчетного времени Tmax - ниже представлены решения для указанных исходных данных для дифференцированного анализа. Так кривые, приведенные на Рис. 7 и иллюстрирующие динамику обеих переменных, с одной стороны достаточно схожи на своих начальных и конечных временных интервалах, а с другой стороны – их значения резко отличаются на средних участках. При этом кривая y(t) сильно «проседает» в районе значения t=1,5. Аналогичную качественную ситуацию иллюстрирует и Рис. 8. Здесь кривая производной от параметра y хоть и «проседает» в таком же временном интервале, но это «проседание» менее выражено. Что касается кривой взаимного соответствия производных по времени от обеих переменных x и y, представленной на Рис. 9, то здесь наблюдается некоторое качественное сходство с кривой соответствия их собственных величин, представленной на Рис. 2, но в данном случае кривизна выражена слабее.
67

68

69 Рис. 7. Временная динамика линейных характеристик двух целевых показателей x и y
70

71

72 Рис. 8. Временная динамика скоростных характеристик двух целевых показателей x и y
73

74 Рис. 9. Годограф скоростей двух целевых показателей x и y
75 Особенностью представленных выше результатов модельных расчетов в соответствии с Табл. 1 является использование в интересах графических иллюстраций как основы максимального характерного (при этом безразмерного) времени развития процесса - Tmax в отличие от размерного расчетного времени t. Последнее в наших расчетах составляет чуть меньше 2 (при Tmax=10). При этом t имеет размерность обратную размерностям коэффициентов при переменных x и y. Например, если t будет иметь размерность секунды, то коэффициенты интенсивностей обратных связей a, b, c, d будут измеряться в герцах (герц - единица, обратная секунде). При этом связь между T и t через модуль максимального значения из двух коэффициентов выглядит следующим образом: ,
76 где λ1,2 являются решениями уравнения (4). При этом λ1,2 имеют размерность обратную времени, т.е. в частном случае – те же герцы. На приведенных выше графиках по оси абсцисс указаны величины именно размерного расчетного времени t.
77 Таким образом, в статье предложен и обоснован методологический подход к описанию инновационной деятельности как саморазвивающейся системы с комплексом социально-экономических прямых и обратных связей разной направленности. В качестве источника обратных связей рассмотрен спектр фундаментальных социальных и экономических противоречий, заложенных в феномене «знания», в свою очередь являющегося итоговым продуктом в условиях современного постиндустриального типа воспроизводства. Разработана математическая модель оценки устойчивости и динамики инновационной деятельности на основе системы неоднородных дифференциальных уравнений первого порядка. При этом модель иллюстрирует отсутствие явного влияния, как институциональной среды, так и инвестиционного климата в виде соответствующих прямых связей, на устойчивость запуска инновационных проектов.
78 Предложенная математическая модель может быть взята за основу при социально-экономическом обосновании инновационных проектов широкого спектра, в том числе при оценке рисков устойчивости их запуска. Кроме того модель позволяет использовать прием диверсификации социальных и экономических ресурсов саморазвития в интересах устойчивости таких проектов.
79 Дальнейшее совершенствование метода предусматривает методологические изыскания в следующих направлениях: - детальной структуризации социальных и экономических прямых и обратных связей; - количественной оценки интенсивностей обратных и прямых социальных и экономических связей; - согласования размерностей переменных в виде социальных и экономических параметров; - учета временной зависимости интенсивностей указанных выше связей; - разработки, с учетом особенностей функционирования предложенной модели, управленческих стратегий, как по дифференциальной, так и по комплексной минимизации отрицательных видов прямых и обратных связей с целью обеспечения устойчивости инновационных проектов.

Библиография

1. Первозванский А.А., Первозванская Т.Н. Финансовый рынок: расчет и риск // М.: Инфра-М, 1994 г. С. 80–81.

2. Лепский В.Е. Саморазвивающиеся инновационные среды в контексте становления VII социогуманитарного технологического уклада / Организация саморазвивающихся инновационных сред // М.: «Когито-Центр», 2012.

3. Бестужев-Лада И.В. О прогнозном обосновании социальных нововведений / Экономическая теория в XXI веке – 7(14): Инновационная экономика // М.: Краснодар, 2008. С. 9–17.

4. Иванова В.Н. Функциональные модели инновационного развития в постиндустриальной экономике // Вопросы новой экономики. 2009. № 4. С.23–32.

5. Иванова В.Н. Знания как форма социальных обратных связей в инновационном развитии /Материалы Международного молодежного научного форума «ЛОМОНОСОВ-2017». [Электронный ресурс] — М.: МАКС Пресс, 2017. Cекция "Социология", подсекция «Экономическая социология».

6. Иванова В.Н. Знания как ключевой ресурс социальных инноваций / Российское системное перестроение как стратегическая неизбежность: неоэкономика, неоиндустриализация, неодирижизм: Сборник тезисов выступлений участников Международной научной конференции // М.: Экономический факультет МГУ им. М. В. Ломоносова, 2016. С. 118–119.

7. Иванова В.Н. Об истоках социальных ограничений в инновационной деятельности / Материалы Международной научной конференции «Россия на пути к России: концептуальный поиск и хозяйственная стратегия»: Сборник тезисов выступлений // М.: Экономический факультет МГУ имени М.В. Ломоносова, 2017. С. 221–223.

8. Иванов А.А. Русские в Российской Федерации (причины социальной дезадаптации) / Экономическая теория в XXI веке – 1(8): Экономика Постмодерна // М.: Экономистъ. 2004. С. 628–636.

9. Иванов А.А. Современная Россия: кризис идентичности / Материалы международной научной конференции в МГУ им. М.А. Ломоносова «Неуемная Россия» // Издательство Волгоградского государственного университета. Москва-Волгоград. 2003. Том 1. С. 230–234.

10. Иванов А.А. «Россияне» как символ системного социального кризиса / Перестроение России. В 2 т. Т.2. // М.; Волгоград: Волгоградское научное издательство, 2010. С.113–122.

11. Иванов А.А., Иванова В.Н. Истоки, структура и функции социальных связей в инновационной деятельности // Философия хозяйства. 2018. № 3 (117). С. 230–244.

12. Фурманс В. Военные отставники идут в корпорации // Ведомости. 12.04.2017. С. 21.

13. Полтерович В., Попов В., Тонис А. Механизмы «ресурсного проклятия» и экономическая политика // Вопросы экономики. 2007. № 6. C. 4-27.

14. Санникова К. Геннадий Воронин: Поправки в ЗАКОН «О Техническом регулировании» – очередная ошибка, он просто НЕ НУЖЕН! // www. angi.ru, 18.12.2009.

15. Перечень действующих Технических регламентов Российской Федерации // http://rostestbarnaul.ru/perechen-dejstvuyushhix-texnicheskix-reglamentov-rf/.

16. Федоров Е. Изменения в закон о техническом регулировании рекомендованы кпринятию // www. legis.ru, 18.12.2009.

17. Фролов Д.П. Институциональная логика технологического прогресса (случай нанотехнологий) // Journal of Institutional Studies - Журнал институциональных исследований. 2012. Т. 4. № 1. С. 49–64.

18. Салихов Б.В., Антипова Д.А. Инновационное мышление и основы механизма управления творческим потенциалом современной корпорации // Транспортное дело России. 2014. № 1. С.205–210.

19. Иванова В.Н. Динамическая модель инновационного развития / Экономическая теория в XXI веке – 8(15): Экономика модернизации: монография // М.; Ростов н/Д: Вузовская книга, 2011. С. 186–192.

20. Иванова В.Н. Научно-технические кластеры как инструмент инновационного развития в рамках эволюционной экономической теории // Экономический вестник Ярославского университета. 2009. № 30. С. –11.

21. Иванов А.А. Иррациональное поведение: истоки, формы, критерии / Современность: хозяйственные алгоритмы и практики. Моск. гос. ун-т им. М.В. Ломоносова // М.; Тамбов: Издательский дом ТГУ им. Г.Р. Державина, 2016. C. 447–457.

Комментарии

Сообщения не найдены

Написать отзыв
Перевести